In today’s fast-paced and ever-evolving world, it is becoming increasingly important for individuals to possess strong mathematical skills. Whether you are an aspiring engineer, a business professional, or even a parent assisting your child with their homework, a solid understanding of mathematical concepts is crucial. To cultivate these skills, educators have developed a set of guidelines known as the Eight Mathematical Practices.
- Problem Solving
- Reasoning and Explaining
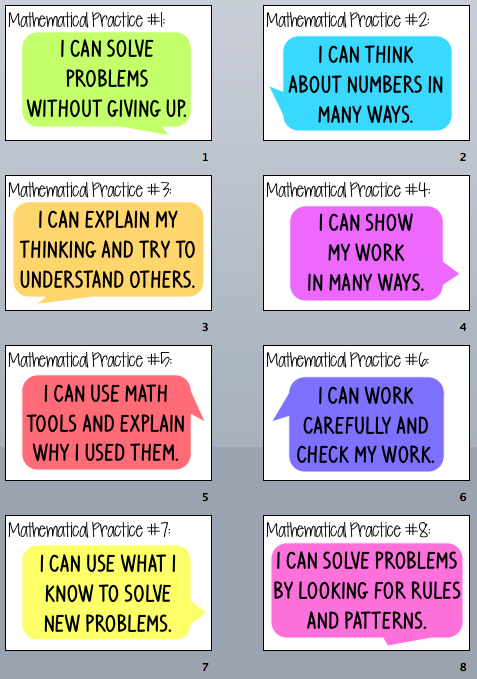Mathematics is not just about arriving at an answer; it is also about being able to justify and explain that answer. This practice emphasizes the importance of providing clear and coherent reasoning. By mastering this skill, individuals are better equipped to communicate their mathematical thoughts and ideas effectively.
- Modeling and Using Tools
Mathematical modeling involves the process of creating representations to solve complex problems. This practice encourages individuals to utilize a variety of tools, such as graphs, diagrams, and technology, to analyze and interpret data effectively. By incorporating real-world scenarios into mathematical problems, students can develop a deeper understanding of how mathematics is applied in various fields.
- Using Precision and Accuracy
Accuracy and precision are fundamental in mathematics. This practice focuses on developing skills to calculate solutions with meticulous attention to detail. By emphasizing the importance of using precise measurements and clear numerical relationships, educators are fostering a strong foundation in mathematical accuracy.
- Finding Structure and Generalizing
Identifying patterns and discovering the underlying structure of mathematical concepts is a key aspect of this practice. By exploring connections between different mathematical ideas, individuals can generalize their understanding and apply it to a wide range of problems. This skill enhances critical thinking and problem-solving abilities.
- Expressing Regularity and Repetition
Consistency and repetition are essential in mathematics, especially when working with complex calculations. This practice highlights the importance of organizing and expressing mathematical ideas in a systematic manner. By establishing regularity and repetition, individuals can enhance their understanding and memorization of important mathematical concepts.
- Connecting Mathematical Representations
Mathematics is often represented in various forms, including graphs, symbols, and equations. This practice focuses on the ability to make meaningful connections between these different representations. By understanding the relationship between various mathematical forms, individuals can better visualize and comprehend mathematical concepts.
- Attending to Precision
Attention to precision is crucial in mathematics as even a small error can lead to significant discrepancies in the final result. This practice encourages individuals to be meticulous and accurate in their calculations, ensuring that their solutions are precise. By being mindful of precision, individuals develop a valuable skill that can be applied to various fields requiring attention to detail.
In conclusion, the Eight Mathematical Practices provide a comprehensive framework for developing strong mathematical skills. By emphasizing problem-solving, reasoning, precision, and the ability to make meaningful connections, educators are equipping individuals with the necessary tools to succeed in the ever-expanding world of mathematics. Whether you are a student, a professional, or a parent, embracing these practices is essential for fostering a deep understanding and appreciation for the power of mathematics.
